Structure de table
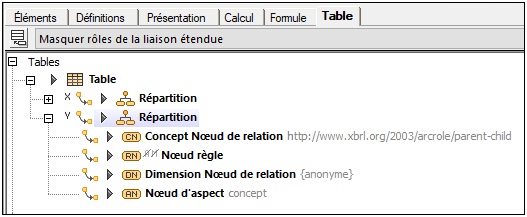
La structure d'une table dans la définition de table est définie par les axes de la table (X,Y,Z) dont chacune d'entre elle correspond à un ou plusieurs composants de répartition (voir capture d'écran ci-dessous).
•Les axes X et Y correspondent, respectivement, aux colonnes et aux lignes de la table générée. Elles sont décrites dans la section, Axes X et Y.
•Si un axe Z est défini, il est présenté en tant que table séparée. Voir la section Axe Z.
•Chaque composant de répartition peut contenir plusieurs nœuds de définition de table (voir capture d'écran ci-dessous). Il existe des types différents de nœuds de définition :
— nœuds de règle (icône RN dans la capture d'écran ci-dessous)
— nœuds de relation de concept (CN)
— nœuds de relation de dimension (DN) et
— nœuds d'aspect (AN).
Voir la section nœuds de définition pour une description des propriétés structurelles de ces nœuds de définition.
Projections pour les répartitions multiples
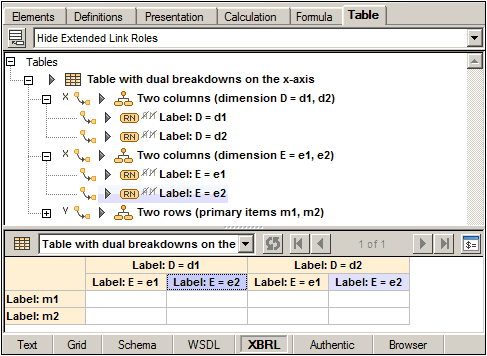
Des répartitions indépendantes multiples peuvent être associées avec une seule axe de table. Le mécanisme pour résoudre comment les répartitions multiples sont combinées dans une seule répartition “effective” s'appelle une projection. La priorité relative des répartitions multiples pour un axe unique est déterminée par l'attribut @order de chaque répartition. Les répartitions sont visualisées en tant qu'arborescences. Pour chaque feuille de la première répartition, toute la deuxième répartition est attachée, etc., récursivement.
Dans la capture d'écran ci-dessous, par exemple, on peut voir deux répartitions pour les axes X : dimension D est classée à une propriété plus élevée que dimension E. Donc, pour chaque feuille de dimension D (d1 et d2) toute l'arborescence de dimension E est attachée. Puisque l'axe X génère des colonnes, ces répartitions créent une projection pour la structure en colonne de la table. Voir l'aperçu de mise en page de la table dans la capture d'écran ci-dessous.